In the first session of our Deep Learning series, we emphasized the importance of human brain inspiration in some of the basic ideas of Deep Learning like, for example, the basic learning unit: the neuron. The human brain and our algorithms are hardly alike, as Neuroscience and Deep Learning are quite different disciplines, but some of the concepts still give support to some ideas. In this post we will talk about one of those ideas: the memory.
To go further on the topic, on 10 October 2017 you have the opportunity to join a Data Science meetup in Madrid which focuses on Deep Learning: confirm your assistance. Also, there will be a surprise at this meetup! One lucky assistant will win a ticket to Big Data Spain, one of the three largest conferences in Europe about Big Data, Artificial Intelligence, Cloud Technologies and Digital Transformation.
Meanwhile, you can continue with the reading… and if you are interested in Deep Learning, you can read our previous tutorials:
Introduction to Deep Learning Part 1: Neural Networks
Introduction to Deep Learning Part 2: Parameters and Configuration

Until now, everything we talked about was based on isolated actions, representations or merely data. When facing a picture classification task between cats and pirates, does a picture of a cat depend on the previous picture of a pirate? Probably not, but if the cat image is a frame in a movie and we identified it two seconds ago, do we expect to see the same cat or something different? And how can we translate it to fit our “brand new” neural nets and learn patterns’ sequences?
Fortunately, the answer to that question is affirmative. Nowadays, there are many applications of Deep Learning to sequence data, from the most widely used like word-prediction when texting or language to language translation, to other less-known ones, which are even more amazing, like images’ text description.
Sequential data, Recurrent Neural Networks and BackPropagation Through Time
Aside from cinematic data, sequences are a very natural way of representing reality: from sight and hearing to behavior and language, but also more artificial kinds of data like, for example, stock exchange information. When applying supervised learning to this, the idea is to try to predict the future taking into account the recent past.
In order to achieve this, we have to adapt the structure of our neural networks. So, the idea is to add a dimension to the picture and let layers grow both vertically and horizontally. Thus, our nets, which now will be called Recurrent Neural Networks (RNN), will have two depths, as in the next picture:
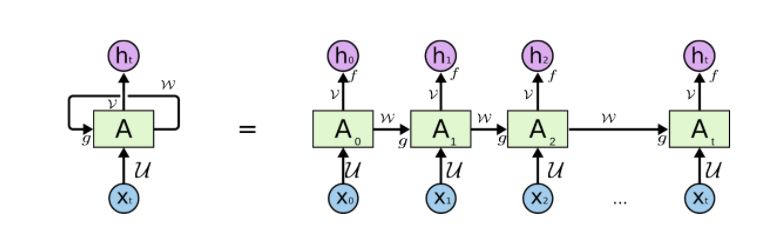
On the right term of the equality (forget the left one for now) each subindex is meant to represent a timestep and, as you can see, there are inputs (Xs) and outputs (hs). Input data respond to sequences [latexpage]$x_{1\cdots t} = (x_1, x_2, \cdots, x_t)$ but each $x_i$ acts as the input in one timestep. So, a sequence $x_{1\cdots t}$ can be used as an input to predict the next in the sequence: the $x$ at timestep $t + 1$. Now, if we look at the picture, for each timestep $i$ the respective $x_i$ has an output $h_i = \hat{x}_{i+1}$, meant to predict $X$ at the timestep $i+1$. Therefore, the real output we are looking for is $h_t = \hat{x}_{t+1}$. But what about the As? This is where the whole action takes place, as they are meant to represent one (or perhaps more) layers in the same sense as in a regular neural network.
As in regular neural networks, there are activation functions and linear operations in RNNs. We denote these linear operations by its matrices $\mathcal{U}$, $\mathcal{V}$ and $\mathcal{W}$. Please let me remark that, in order to keep the time structure, matrices $\mathcal{U}$, $\mathcal{V}$ and $\mathcal{W}$ are shared along the timesteps. So, we have:
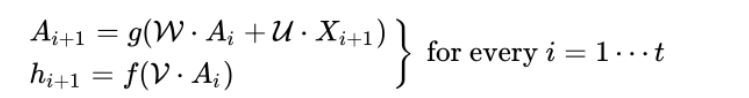
Where f and g stand for the activation functions (as you’ll remember, sigmoid, relu, tanh, etc) which are also shared along the timesteps (this is the key to the “folded” representation or the term in the left of the previous equality). So, in order to make the whole thing work out, we have to find the optimal parameters for the matrices and, to achieve that, we will use an analogous version to backprop: the BackPropagation Through Time (BPTT). As in the single-step ordinary backprop, we have to minimize a loss function, which in this case is:
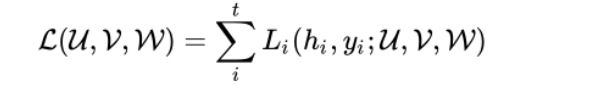
Where each $L_i$ stands for the regular loss function on each timestep, as we computed for the ordinary case. On each timestep, the network parameters depend on the parameters on the previous timestep and, as you may imagine, so do the derivatives. This implies a wide use of the chain rule and that derivations may end up being computed in terms of several timesteps.
Long Short Term Memory (LSTM) Networks. The Vanishing Gradient.
Until now we have introduced some memory into Neural Nets, but if we take a look again to the unfolded RNN, it seems that the very recent past is much more important than the more distant events, since information can be diluted over the timesteps. Numerically translating, timestep-composition of derivatives may lead into what is called the Vanishing (or exploding) Gradient. For further information of this concept, please allow me to redirect you to the video for this season.
However, in order to solve this problem, we can once again, make use of human brain intuitions. For instance, if we go back to the cat example at the beginning, we mentioned a time-continuous memory: in the very next future we expect to see something similar to what we just saw, but if we first met our cat (who, from now will be called ”Calcetines”) in a couple of scenes some minutes ago, the next time we see a fluffy tail, we will probably associate it with Calcetines. This association, along with the “time-continuous” one, are two quite different kinds of memory association, and they are called Long (resp. Short) Term Memory.
This idea originate the LSTM nets, which share the general RNN schema, but also include both memories as connections:
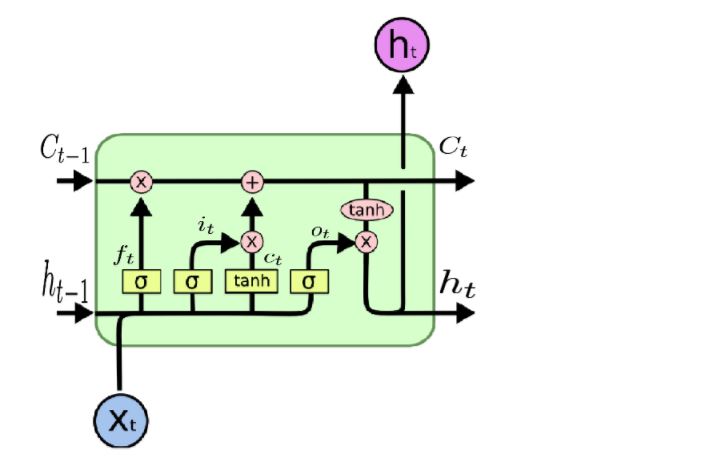
In the picture above, $h_{t-1}$, $h_t$ and $C_{t-1}$, $C_t$ represent the Short and the Long Terms respectively. Each LSTM cell corresponds to a timestep, and receives both terms from the previous timestep/cell in addition to the corresponding input $x_t$. Inside each cell there are four “gates”, whose function is to determine which part of the Long and Short Memories to delete, which to store and which to use on the output. As in the RNN case, cells are timewise connected, and backprop on LSTM is similar to the RNN one.
LSTM architectures are widely used on sequential data problems, obtaining fair results in most cases, specially in the ones related to natural language.

To summarize, in this post we made a first approach to the use of Deep Learning on sequential data problems. We defined the classic Recurrent Neural Networks architecture and introduced the Long and Short Term Memory concept, as a possible solution for the Vanishing Gradient Problem. This leads to the LSTM architecture, originally conceived by Sepp Hochreiter and Jürgen Schmidhuber in 1997.
Sequential data is everywhere and it has a lot of outstanding applications. Text generation is one of them. Simple sentences can be easily generated from a not-so-deep LSTM network trained on books or wikipedia, but deeper and more complex networks have proved to be able to write a whole movie (short-film) script. The result is quite nonsensical as a whole compared to human written scripts, but it gives us a taste of the high potential behind LSTM networks.
In the next sessions we will talk about how to deal with images in Deep Learning, using the Convolutional Neural Networks. Watch this video and find out more!




