This is the second (and last) part of the series dealing with the formal comparison of Machine Learning (ML) algorithms from a statistical point of view. In this post, we examine how statistical tests are applied to performance data of ML algorithms.
Application of statistical tests to algorithm performance data
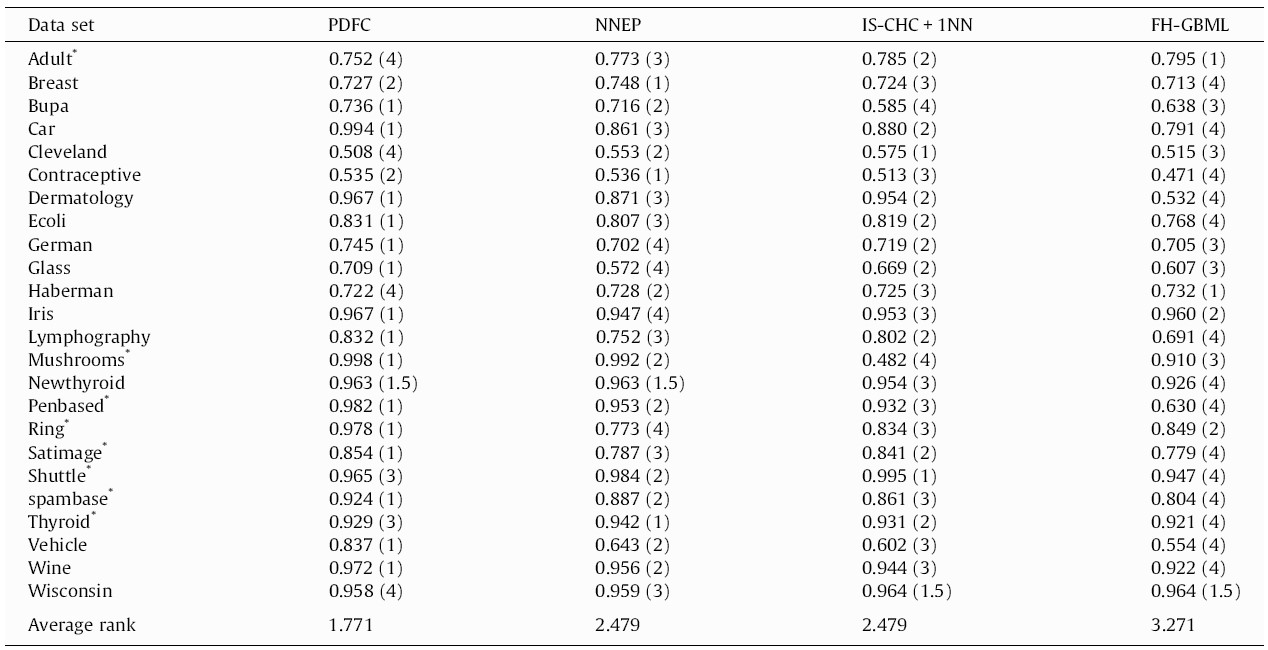
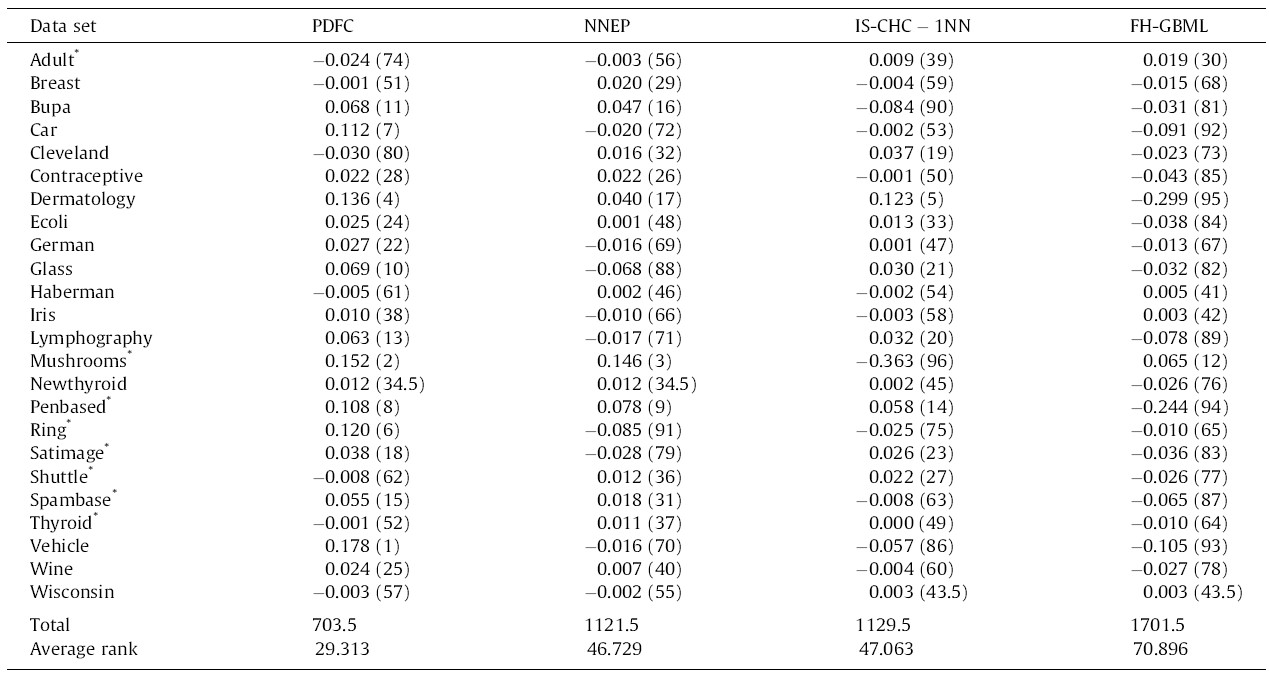
Let’s assume that we have performance data (for instance, the AUC or the F-measure) of multiple algorithms (instead of medicines) on multiple datasets (instead of patients), like in Table 1 (reproduced from [3]). The column names represent four different ML algorithms, while the rows are datasets on which they were tested. In research articles, it is common to use well-known datasets (most of them with real-world data collected in real studies) from open databases, such as the UCI ML Repository. Parentheses indicate the rank per dataset, needed in Friedman.
Friedman’s two-way (repeated measures) analysis of variance by ranks
Secondly, we are applying the algorithms to exactly the same dataset (the latter are the experimental unit here), so the results are paired per dataset (per row of the table). The statistical test that is commonly used in this case is called Friedman’s two-way analysis of variance by ranks [see 3, 4]. Friedman’s test statistic is:
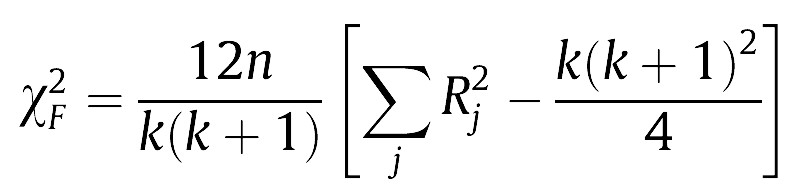 (1)
(1)
A corrected version was later proposed by Iman and Davenport:
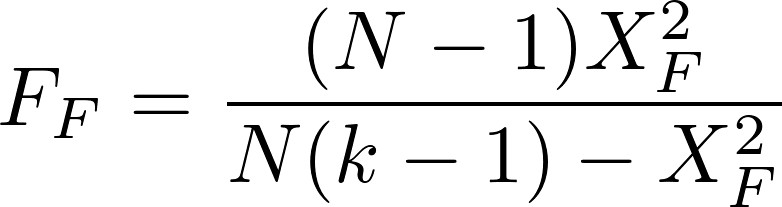 (2)
(2)
In Eq. (1), the test statistic follows a Chi-square distribution with k-1 degrees of freedom under the null hypothesis when n and k are big enough (n > 10, k > 5), as stated in [3], where n is the number of datasets and k is the number of algorithms being compared. Rj stands for the average rank of algorithm j (in Table 1, R1 = 1.771, R2 = 2.479, R3 = 2.479, R4 = 3.271). In Eq. (2), the test statistic follows an F distribution with k-1 and (k-1)(n-1) degrees of freedom (in our case, 3 and 69) under the null hypothesis of equal performance of all algorithms. If you do the maths, you will find that X2F = 16.225 and FF = 6.691, the latter having a very low p-value according to an F3,69 distribution. Hence we reject the null hypothesis which states that all algorithms have the same performance, and conclude that at least one of them behaves differently.
Friedman’s aligned ranks test and Quade’s test
As stated in [3], Friedman’s test ignores a lot of information, and since the a rank is built per dataset, it is not possible to compare them across multiple datasets. A variant known as Friedman’s aligned ranks test first computes the average performance of all algorithms in a dataset, and subtracts this value from the individual performances to see which algorithms are above or below the average performance at each dataset. A single global rank is built according to such differences, which are called aligned ranks (Table 2). According to [3], when using the aligned ranks “…the ranking scheme is the same as that employed by a multiple comparison procedure which employs independent samples”. The Friedman aligned ranks test statistic is:
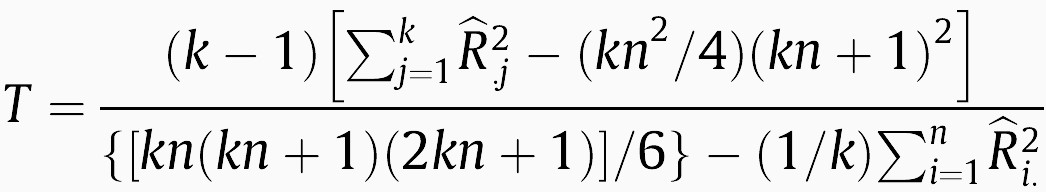 (3)
(3)
where R̂i.2 is equal to the rank total of the i-th data set and R̂.j2 is the rank total of the j-th algorithm. Under the null hypothesis of equal performance of all algorithms, T follows a chi-square distribution with k-1 degrees of freedom.
When Friedman’s test is able to reject the null hypothesis, we must go ahead and check which algorithm is better or worse than each other by doing pairwise statistical comparisons. Since we are going to compare two samples each time (one vs one for all combinations), we use a statistical test for two samples and apply it repeatedly for every combination of two samples – this is known as conducting a post-hoc test.
Post-hoc analysis after Friedman’s test, and the concept of p-value
The problem of comparing two paired populations that do not meet parametric assumptions can be solved in various ways. One can apply a conventional non-parametric two-sample test for paired samples such as Wilcoxon’s signed rank test to every comparison of two samples, for instance. However, if either Quade’s test or any variant of Friedman’s test were applied previously, one can re-use the computations to obtain a statistic that can be used for pairwise comparisons in a post-hoc test. We provide below the expressions to compute such statistic after Friedman’s test when comparing algorithm i vs algorithm j. The reader interested in the expression of a post-hoc test after Quade’s test can find it in [3].
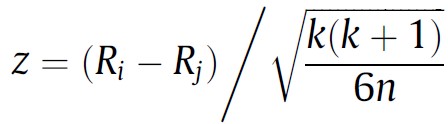
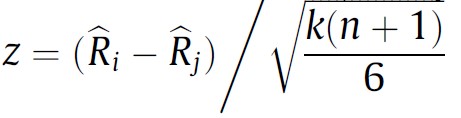
In both cases, the z statistic follows a N(0, 1), i.e. a normal distribution with mean 0 and variance 1 (called the standard normal distribution) when the null hypothesis is true (a.k.a under the null hypothesis).
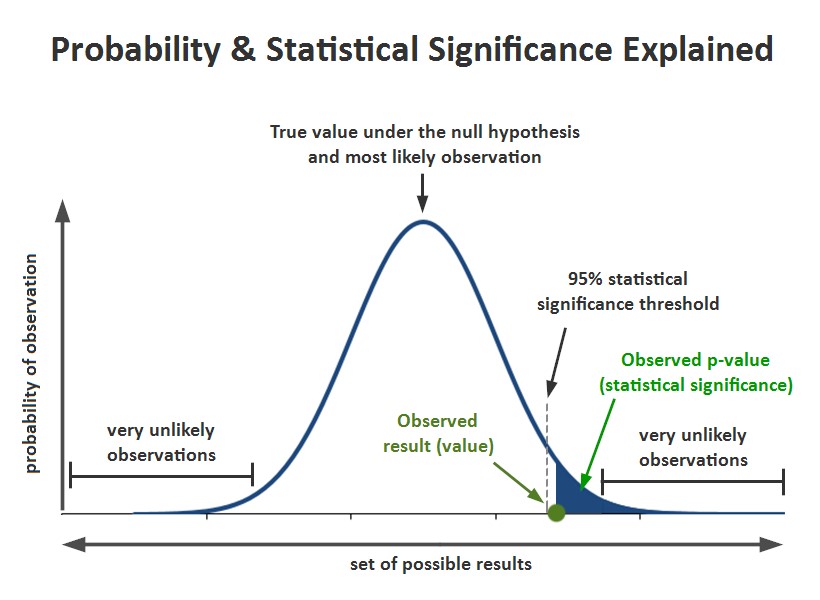
And, although we have already mentioned it in the result of Friedman’s test, we have to stop here and discuss the concept of a p-value. In a statistical test, we build a statistic (which is basically an expression involving our data), which is actually a random variable that is known to follow certain probability distribution when the null hypothesis of the test (i.e. the hypothesis stating the opposite of what we want to prove) is true. In the post-hoc analysis example, the null hypothesis states that both samples come from the same population, and we are interested in rejecting that hypothesis because it is not compatible with our data.
Since the value of our statistic in our problem (i.e. when the expression is evaluated with our specific data) can be considered as a realization of the random variable constituted by the statistic, we can check how likely it is to get such value according to the probability distribution of our statistic under the null hypothesis. If it is extremely unlikely to get such value when we sample from the statistical distribution followed by the statistic under the null hypothesis, then we conclude that “we were wrong in our initial assumption and therefore the statistic does not follow such distribution”. In practice, this is means that our null hypothesis does not hold (it is false).
A p-value is the probability of obtaining a value that is equal to or more extreme than our observed value when sampling from the probability distribution followed by our statistic under the null hypothesis. Formally, it is the Pr(our statistic >= our observed value). When should we consider the p-value low enough to reject the null hypothesis? A general threshold of 0.05 is established so that the null hypothesis happens to be true only 5 % of the times that we end up rejecting it by mistake. It is also very common to pre-compute the value of the statistic at the threshold point of 0.05 because under the null hypothesis, any value greater than such limit has a probability of less than 0.05 of appearing.
P-value adjustment for multiple pairwise comparisons
When we set a threshold of 0.05 to consider the p-value as low enough, we admit that there is a 5 % chance of incorrectly rejecting the null hypothesis when it is actually true (this is known as committing a type I error). But if we do multiple pairwise comparisons and we want to have 5 % chance of making a mistake globally, then we must adjust the p-value for multiple comparisons. This must be done whenever we are conducting multiple comparisons, no matter the statistical test where the p-values came from. Basically there are two approaches for this: adjusting the p-value of each comparison, or leaving the p-values unchanged but adjusting the significance threshold to be much less than 0.05. The exact procedures to achieve this are beyond the scope of this article, but the interested reader can search for methods like Hochberg (the most common), Holm, and Bonferroni among others (again, see [3] for more details).
What we must keep in mind is that any problem in which we want to do pairwise statistical comparisons and get an ordering always needs p-value adjustment.
With this, we can determine, from a statistical point of view, which algorithm works better or worse than any other, and our conclusions will not be subjective but supported by the strength of inferential statistics.
References
[1] Demšar, J. Statistical comparisons of classifiers over multiple data sets. Journal of Machine Learning Research 7:1-30 (2006).
[2] García, S., and Herrera, F. An extension on statistical comparisons of classifiers over multiple data sets for all pairwise comparisons. Journal of Machine Learning Research 9:2677-2694 (2008).
[3] García, S., Fernández, A., Luengo, J., and Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Information Sciences 180:2044–2064 (2010).
[4] Daniel, W. W. “Friedman two-way analysis of variance by ranks”. Applied Nonparametric Statistics (2nd ed.). Boston: PWS-Kent. pp. 262–74. ISBN 0-534-91976-6 (1990).
[5] Quade, D. Using weighted rankings in the analysis of complete blocks with additive block effects, Journal of the American Statistical Association 74:680–683 (1979).




